Math for Kindergarten – Make Ten

B&W + Color printables

This download is available to members only.

Gain Unlimited Access to All Printables!

Already a member? Log-in here.

$kindergarten math addition worksheets with pictures$

$kindergarten math addition and subtraction worksheets$

Lesson plan created by –

Alfred Lewis

Lesson Title	Lesson 10 – Make Ten
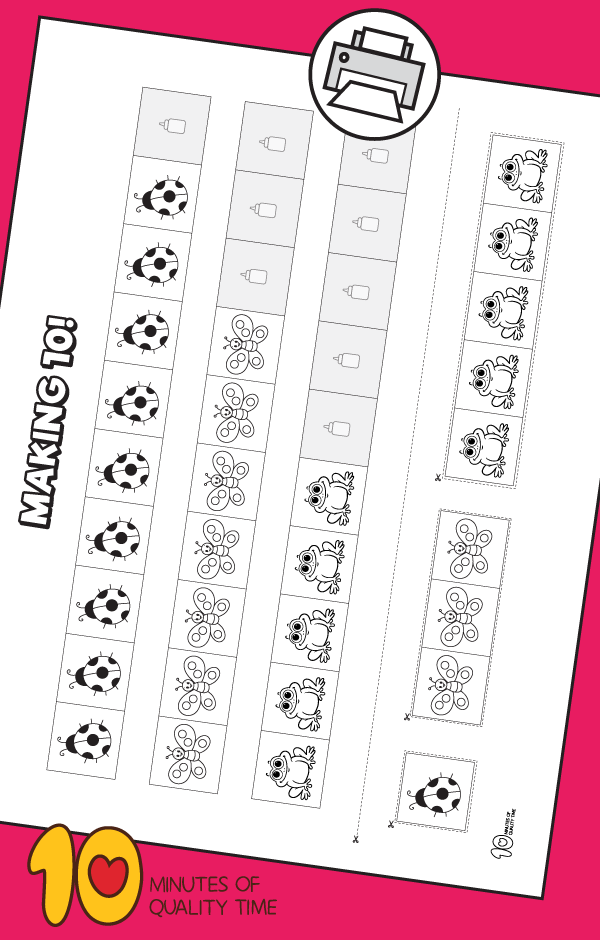
Standards	K.OA.A.4 For any number from 1 to 9, find the number that makes 10 when added to the given number, e.g., by using objects or drawings, and record the answer with a drawing or equation.
Materials Needed	Printable – Groups of Animals (All less than ten with missing spaces to complete the set to make ten) Crayon Pencil Scissors Glue Stick
Teacher Directions	Review counting to ten Pass out the printable Show a group of nine. Ask students to count how many more to make ten Repeat process for 7 & 5. Model for students how to cut out and paste enough animals to complete the set of ten. You can cut out the animals seperately to practice other numbers as well. Model writing the number they cut and pasted. Early finishers can color the sets they created.
Guiding Questions	“How do we count on to make ten?” “How does addition help us make groups of ten?”“How do you know this number is smaller?”
Assessment	Monitor student work on printable